https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
이 문제는 세그먼트트리를 이용하는 문제이다.
세크먼트 트리는 주어진 쿼리를 빠르게 처리하기 위한 자료구조로 여기서는 구간합을 구하는 용도로 사용되었다.
예를들어 1~10까지의 수가 있고 이중에서 몇몇 값들을 바꾸어서 구간의 합을 구하는 경우에 아래의 그림과 같은 세그트리를 만들 수 있다.
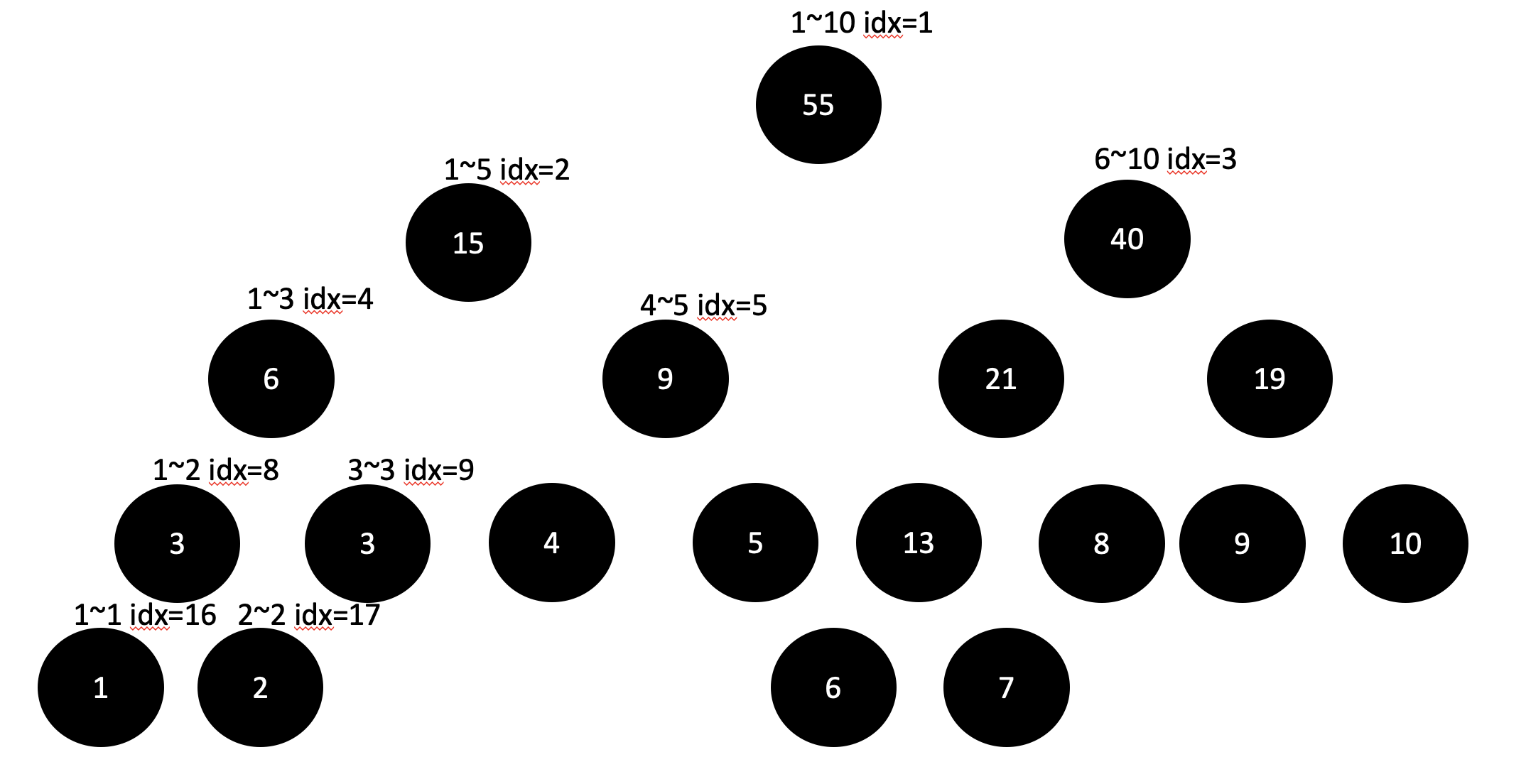
각각의 노드에는 구간의 합을 저장하여 필요에 따라 구간합을 구하는 트리 구조이다.
예를 들어 5~8의 구간 합을 구한다면, 5+21로 구할 수 있다. 평범한 배열구조였다면, 5+6+7+8로 구해야한다.
그리고 값을 바꿀때는 구간합을 모두 갱신해주는 방법으로 값을 바꾼다.
그래서 초기화와 구간합, 갱신 모두 재귀함수를 이용하여 트리구조를 구성한다.
여기서 생각할 것은 왼쪽 자식은 idx*2이고 오른쪽 자식은 idx*2+1이라는 것이다.
자식노드의 위치와 구간 범위 조건만 잘 활용한다면 세그트리를 구현할 수 있다.
또하나 주의 할 것은 트리의 크기인데 트리의 크기는 주어진 배열보다 큰 가장작은 정수의 제곱의 2배이다. 10의 경우 가장 가까운 제곱수는 16이고, 이것의 두배인 32로 트리의 크기를 설정하면 된다. 그래서 크기는 보통 주언진 수열의 4배를 한다.
먼저, 초기화하는 로직은 아래와 같다.
public long init(int start, int end, int idx){
if(start==end){
tre[idx]=arr[start];
return tre[idx];
}
int mid = (start+end)/2;
tre[idx]=init(start,mid,idx*2)+init(mid+1,end,idx*2+1);
return tre[idx];
}트리의 초기화 로직과 비슷하다. 다른 점은 부모의 노드에 자식노드의 합을 넣는 것이다.
그다음으로 구간합을 구하는 로직은 아래와 같다.
public long interval_sum(int start, int end, int idx, int left, int right){
if(left>end || right<start){
return 0;
}
if(left<=start && end<=right){
return tre[idx];
}//구간이 배열 전체를 포함하고 있는 경우
int mid = (start+end)/2;
return interval_sum(start,mid,idx*2,left,right)+interval_sum(mid+1, end, idx*2+1,left,right);
}주어진 구간이 전체 배열의 시작과 끝의 범위를 벗어나면 합은 없다.
합을 구하는 조건은 구간이 배열을 포함하고 있는 경우로 이때는 노드의 값이 구간의 합이 된다.
이 조건이 아닐 경우는 계속해서 탐색한다.
그다음 갱신 로직은 아래와 같다.
public void update(int start, int end, int idx, int what, long value){
if(what<start || what>end){
return;
}
tre[idx]+=value;
if(start==end){
return;
}
int mid = (start+end)/2;
update(start,mid,idx*2,what,value);
update(mid+1,end,idx*2+1,what,value);
}이 문제에서 주의 할 것은 주어진 값을 다른 값으로 바꾸는 것이기 때문에 원래값과 변경 값의 차를 전체 노드의 구간합에 더해준다.
예를 들어 2을 6으로 바꾼다고 하면, 4를 더해주는 것이다.
이 문제를 풀면서 시간을 소비하고, 어려웠던 것은 numberFormatError인데, 이는 갱신하려는 과정에서 들어오는 값이 int범위를 벗어나는 값이 들어 올 수 있어서이다. 따라서 b는 long타입으로 입력받는다.(배열과 트리 또한 long타입으로 바꾸어 주었다.)
그리고 갱신하는 과정에서 변경값과의 차를 구해야하기 때문에 arr의 값도 b->c로 갱신해주어야한다.
정답 코드는 아래와 같다.
package backjoon.b2042;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class b2042 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
long[] arr = new long[N+1];
StringBuilder sb = new StringBuilder();
for(int i=1; i<=N; i++){
arr[i]= Long.parseLong(br.readLine());
}
tree t = new tree(N,arr);
t.init(1,N,1);
for(int i=0; i<M+K; i++){
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
long c = Long.parseLong(st.nextToken());
if(a==1){
t.update(1,N,1, b,c-arr[b]);
t.arr[b]=c;
}else {
sb.append(t.interval_sum(1,N,1, b, (int) c)).append("\n");
}
}
System.out.println(sb);
}
}
class tree{
long[] tre;
long[] arr;
public tree(int N, long[] arr) {
tre=new long[N*4];
this.arr = arr;
}
public long init(int start, int end, int idx){
if(start==end){
tre[idx]=arr[start];
return tre[idx];
}
int mid = (start+end)/2;
tre[idx]=init(start,mid,idx*2)+init(mid+1,end,idx*2+1);
return tre[idx];
}
public long interval_sum(int start, int end, int idx, int left, int right){
if(left>end || right<start){
return 0;
}
if(left<=start && end<=right){
return tre[idx];
}//구간이 배열 전체를 포함하고 있는 경우
int mid = (start+end)/2;
return interval_sum(start,mid,idx*2,left,right)+interval_sum(mid+1, end, idx*2+1,left,right);
}
public void update(int start, int end, int idx, int what, long value){
if(what<start || what>end){
return;
}
tre[idx]+=value;
if(start==end){
return;
}
int mid = (start+end)/2;
update(start,mid,idx*2,what,value);
update(mid+1,end,idx*2+1,what,value);
}
}'CS 이론 > 알고리즘' 카테고리의 다른 글
| 11404번(플로이드 워셜) (0) | 2023.03.01 |
|---|---|
| 1956번(플로이드 워셜) (1) | 2023.02.28 |
| 2293번 (0) | 2023.02.25 |
| 24313번 (0) | 2023.02.22 |
| 9466번(사이클 찾기) (0) | 2023.02.21 |