1753번

https://www.acmicpc.net/problem/1753

1753번: 최단경로

이 문제는 상당히 오래 걸린 것 같다. 다익스트라를 알지 못해서 무작정 BFS로 풀려고 하다보니 많은 시간을 허비하고 시간초과와 메모리 초과의 늪에서 못나오다가 결국 다익스트라 알고리즘을 공부했다.

 

다익스트라 알고리즘의 원리는 간단하다.

1. 출발지점을 설정한다.

2. 출발 지점을 기준으로 각 인접 노드에 접근하는 최소 비용을 저장한다.

3. 방문하지 않은 노드 중에서 가중치가 가장 적은 노드를 방문한다.

4. 해당 노드를 거쳐서 특정 노드로 가는 경우를 고려하여 최소 비용을 갱신한다.

5. 3~4번을 반복하여 진행한다.

 

위 내용처럼 설명하면 이해하기 힘들 수도 있다.

예를 들어 설명하면, 아래 그림과 같은 그래프가 있다고 해보자.

 

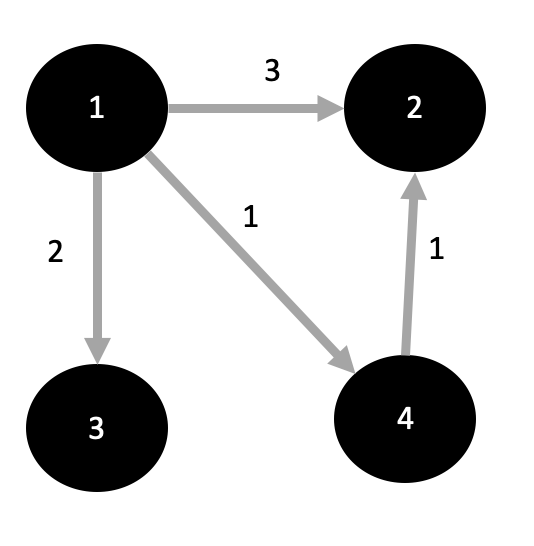
시작 노드는 1이다. 최소 가중치 저장 배열 = {0,MAX_VALUE,MAX_VALUE,MAX_VALUE}

그럼 먼저 큐에 1을 집어넣고 가중치는 0으로 넣는다. 큐:(1,0)

현재 노드의 가중치가 저장된 노드의 최소 가중치보다 크다면 넘어간다.

노드 1과 인접한 2,3,4를 탐색할 것이다.

먼저 2를 봤을 때, 노드 1의 가중치+노드 2의 가중치(=0+3)이 최소 가중치를 저장하는 배열에 노드 2값과 비교했을 때 3<MAX_VALUE이기 때문에 최소 가중치 배열에 3을 저장한다. {0,3,MAX_VALUE,MAX_VALUE}

그리고 큐에도 노드 2에 대해서 가중치 3으로 집어 넣는다. 큐:(2,3)

그 다음 3을 봤을 때 위 과정과 마찬가지로 노드1의 가중치+노드3의 가중치(=0+2)가 배열에 저장된다.

{0, 3, 2, MAX_VALUE}

그리고 큐에도 노드 3에 대해서 가중치 2로 집어 넣는다. 큐:(2,3),(3,2)

그 다음 4를 봤을 때도 마찬가지로 노드1의 가중치+노드4의 가중치(=0+1)가 배열에 저장된다.

{0,3,2,1}

그리고 큐에도 노드 4에 대해서 가중치 1로 집어 넣는다. 큐:(2,3),(3,2),(4,1)

그런 다음 가중치가 가장 작은 (4,1)을 뽑아 낸다. 큐:(2,3),(3,2)

그러면 4와 인접한 2에 대해서 가중치를 계산하는데 노드4의 가중치+노드2의 가중치(=1+1)

이 때 계산한 값이 배열에 저장된 노드 2로가는 가중치 3보다 작음으로 가중치 값을 2로 바꾸어준다.

{0,2,2,1}

그 다음 큐에서 다음으로 가중치가 작은 (3,2)를 뽑아낸다.

이때 3의 인접 노드는 없음으로 넘어간다.

그 다음 큐에 남은 (2,3)을 뽑아내고

인접 노드가 없음으로 마찬 가지로 넘어간다.

 

이번에는 문제에 주어진 예제를 봐보자.

 

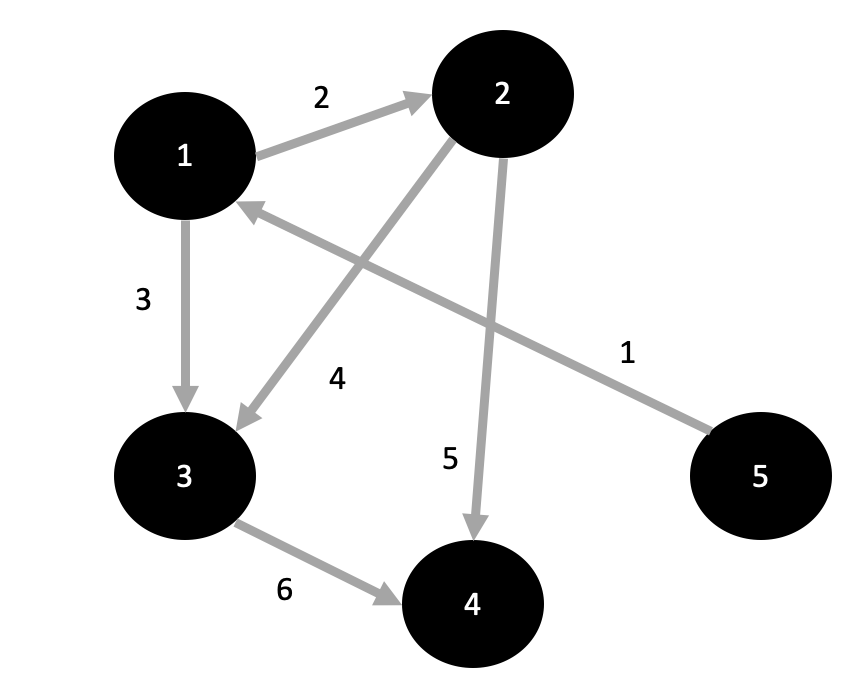
시작 노드는 1이다. 가중치 배열={0, MAX_VALUE, MAX_VALUE, MAX_VALUE, MAX_VALUE}

1의 인접 노드 2,3을 봐보자.

2를 먼저 보면, 1의 가중치+2의 가중치 = 2 {0,2,MAX_VALUE,MAX_VALUE,MAX_VALUE}

3을 보면, 1의 가중치+3의 가중치 = 3 {0,2,3,MAX_VALUE,MAX_VALUE} 큐:(2,2),(3,3)

큐에서 2를 빼면, 큐:(3,3)

2의 인접 노드 3,4를 봐보자.

3을 먼저 보면, 2의 가중치+3의 가중치=2+4=6 배열에 저장된 가중치보다 크다 넘어간다.

4를 보면, 2의 가중치+4의 가중치 = 2+5=7 배열에 가중치보다 작으니까 넣어준다. {0,2,3,7,MAX_VALUE}, 큐:(3,3),(4,7)

큐에서 3을 빼면, 큐:(4,7)

3의 인접한 4를 보면

3의 가중치 + 4의 가중치 = 3+6 = 9 배열의 가중치 보다 크다 넘어간다.

큐에서 4를 빼면, 4의 인접 노드는 없으니 넘어간다.

그럼 배열은 {0,2,3,7,INF}가 된다.

 

정답 코드는 아래와 같다.

package backjoon.b1753;

import java.util.*;
import java.io.*;
public class b1753 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int V = Integer.parseInt(st.nextToken());
        int E = Integer.parseInt(st.nextToken());
        int R = Integer.parseInt(br.readLine());
        List<Node>[] list = new List[V+1];
        for(int i=0; i<=V; i++){
            list[i]=new ArrayList<>();
        }
        for(int i=0; i<E; i++){
            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());
            int weight = Integer.parseInt(st.nextToken());
            list[start].add(new Node(end,weight));
        }
        Graph g = new Graph(list,V);
        g.bfs(R);
        StringBuilder sb = new StringBuilder();
        for(int i=1; i<=V; i++){
            if(g.dist[i]==Integer.MAX_VALUE){
                sb.append("INF").append("\n");
            }else sb.append(g.dist[i]).append("\n");
        }
        System.out.println(sb);
    }
}
class Graph{
    List<Node>[] adj;
    int[] dist;
    PriorityQueue<Node> queue;
    public Graph(List<Node>[] list, int N){
        this.adj=list;
        dist=new int[N+1];
        queue = new PriorityQueue<>();
        Arrays.fill(dist,Integer.MAX_VALUE);
    }
    public void bfs(int R){
        queue.add(new Node(R,0));
        dist[R]=0;//시작 노드의 가중치를 0으로 한다.
        while (!queue.isEmpty()){
            Node node = queue.poll();//시작지점 노드를 빼온다.
            if(dist[node.end]<node.weight)continue;
            //node.end=현재 노드의 저장 되어 있는 최소 가중치
            //즉, 큐에서 꺼낸 노드의 현재까지 계산 해놓은 최소 가중치보다 큐에서 꺼낸 노드의 가중치가 크면 넘어간다.

            for (Node nextNode : adj[node.end]) {//인접 노드를 확인한다.
                int dis = node.weight+nextNode.weight;//현재 노드의 가중치+다음 노드의 가중치
                if(dist[nextNode.end]>dis){//다음 노드의 최소 가중치보다 현재 계산한 다음 노드의 가중치가 작으면 갱신
                    dist[nextNode.end]=dis;
                    queue.add(new Node(nextNode.end, dis));
                }
            }
        }
    }
    /**
     * 1.출발 노드를 설정
     * 2.출발 노드를 기준으로 각 인접 노드의 최소 비용을 저장
     * 3.방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택
     * 4.해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소비용 갱신
     * 5.위 과정에서 3~4번 반복
     */
}
class Node implements Comparable<Node>{
    int end;
    int weight;

    public Node(int end, int weight) {
        this.end = end;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return Integer.compare(this.weight,o.weight);
    }
}